Czy widziałeś kiedyś na jakimś forum lub grupie społecznościowej jak “wysocy rangą” programiści zakazują używać floata? Czy zauważyłeś, że nikt z nich nie tłumaczy dlaczego? Nie bo nie! Tyle. Dlaczego używanie floata dla niektórych osób jest równie złe co zabijanie małych zwierzątek? Sprawdźmy to!

W tym wpisie będę bazował na dokumentacji od ST  AN4044 - Floating point unit demonstration on STM32 microcontrollers.pdf . Dla niektórych dokument ten może być niezorzumiały dlatego pozwól, że trochę rozjaśnię temat floatów dla STM32 i nie tylko.

Reprezentacja float

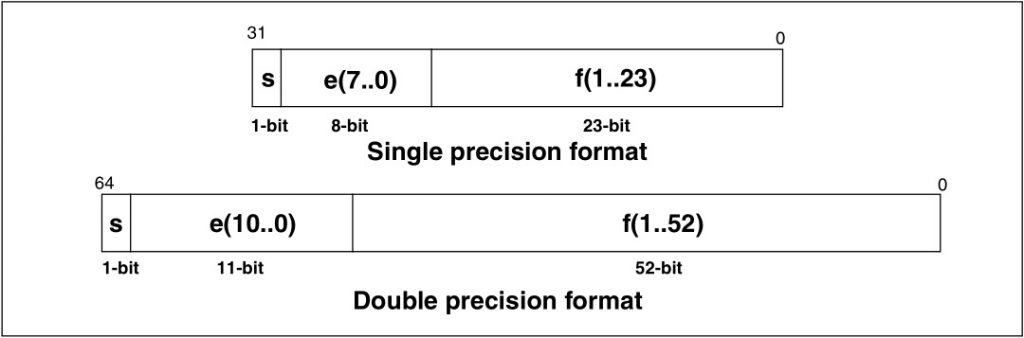
Na początku wypadałoby powiedzieć jak liczby zmiennoprzecinkowe są zapisywane przez MCU. Jak dobrze wiadomo, bit ma tylko dwa stany i nie można pomiędzy 10 a 11 wstawić żadnej liczby ułamkowej. Więc jak to się dzieje? Istnieje bowiem standard arytmetyki IEEE.754 który definiuje zapis oraz podstawowe operacje na float’ach. Najczęściej używane liczby zmiennoprzecinkowe to pojedynczej oraz podwójnej precyzji – single oraz double. Ich zapis wygląda tak:

Co to oznacza?

s – bit znaku. Decyduje o tym czy liczba jest dodatnia czy ujemna. 0 – dodatnia, 1 – ujemna.

e – 8 lub 11-bitowy wykładnik. Całkowita liczba do której podnosimy bazę systemu liczbowego – w naszym przypadku liczbę 2 bo kodujemy binarnie. Do wykładnika należy dodać tzw. bias równy 127 dla single i 1023 dla double.

f – 23 lub 52-bitowa mantysa. Liczba z której uzyskujemy ułamek. Jest to liczba znormalizowana, o czym za chwilę.

Wzór na liczbę zmiennoprzecinkową wygląda wieć następująco:

Wygląda skomplikowanie, co nie? Spróbujmy przekształcić jakiś ułamek na reprezentacje float. Niech będzie to liczba 243.45.

W pierwszej kolejności należy zająć się liczbą całkowitą 243 co jest dosyć proste. Wynik to 11110011. Gorzej jest z ręcznym przekształceniem 0.45. Polecam obejrzeć film tłumaczący jak to zrobić(link). 0.45 w reprezentacji binarnej to 011100(1100…).

Więc 243.45 = 11110011.011100(1100…)

Teraz trzeba znormalizować tą liczbę. Liczba znormalizowana to taka, która znajduje się w przedziale prawostronnie otwartym [1, B) gdzie B jest podstawą kodowania liczby. W naszym wypadku kodowanie jest binarne, więc przecinek musi znajdować się za pierwszą jedynką. Policz o ile miejsc przesunąłeś przecinek. Potrzebne jest to do zapisu wykładnika.

Po znormalizowaniu nasza liczba to 1.110011011100(1100…) x 10^7.

Dzięki temu, że częśc całkowita zawsze wynosi 1, nie ma potrzeby jej pamiętania. W liczbie float zapisywana jest tylko część po przecinku i jest to mantysa skrócona do 23 lub 52 bitów.

f = 11001101110011001100110

Teraz wykładnik. Przesunąłem przecinek o 7 miejsc w lewo, więc wynosi on 7. Dodając do niego bias  dla 32-bitowej reprezentacji wychodzi 134, czyli binarnie 10000110.

e = 10000110

Liczba jest dodatnia, więc znak wynosi zero

s = 0

Teraz można poskładać naszego floata.

243.45 (dec) = 0 10000110 11001101110011001100110 (float)

Proste co nie? 🙂

Operacje na zmiennym przecinku

Standard IEEE.754 definiuje też arytmetyke liczb zmiennoprzecinkowych. Zawiera ona 6 operacji na liczbach:

• Dodawanie
• Odejmowanie
• Mnożenie
• Dzielenie
• Reszta z dzielenia
• Pierwiastek kwadratowy

Spróbujmy czegoś łatwego, np dodajmy do siebie 188.1 i 182.69. W głowie można szybko policzyć, że będzie to 370.79, ale czy float da taki sam wynik?

188.1

188 binarnie to 10111100 natomiast 0.1 jest równoznaczne z 0(0011…). Widzisz małe niebezpieczeństwo związane z nieskończonym rozwinięciem? Jesli nie to spokojnie, będzie widać. Łącząc dwie składowe otrzymuję 10111100.0001100110011(0011) a dostosowując to do standardu float 1.01111000001100110011001|10011 x 10^7. To po pionowej kresce jest nadmiarowe dla float32 i przepada bezpowrotnie. Mamy pierwszą utratę informacji. Wykładnik wynosi 7, więc po dodaniu biasu wychodzi 134.

188.1(dec) = 0 10000110 01111000001100110011001(float)

Teraz 182.69

182 = 10110110.10110000101000111101 = 1.01101101011000010100011|1101 x 10^7

Znowu tracimy informacje o rozwinięciu ułamka. Zamieniając na reprezentację IEE.754:

182.69(dec) = 0 100000110 01101101011000010100011(float)

Pierwsze co należy zrobić przy dodawaniu liczb zmiennoprzecinkowych jest zrównanie ich wykładników. W moim przykładzie mamy te same wykładniki, więc nie trzeba wykonywać tej operacji. Kolejnym etapem jest dodanie do siebie mantys mając w pamięci jedynkę przed kropką, której nie ma w zapisie float. Pominę proces ręcznego dodawania binarnego dla czytelności

1.01111000001100110011001 x 10^7 + 1.01101101011000010100011 10^7 = 10.11100101100101000111100 x 10^7

Wynik należy znormalizować: 1.01110010110010100011110|0 x 10^8

W zapisie float nasz wynik wygląda tak: 0 100000111 01110010110010100011110

Należałoby rozszyfrować ten wynik. Najłatwiej będzie mi wyciągnąć go ze znormalizowanego wyniku oczywiście uciętego do rozmiarów standaru float bo to z niego de facto wyciągamy wynik działania.

1.01110010110010100011110 x 10^8 = 101110010.110010100011110

Rozbijam to na część całkowitą i ułamkową:

101110010 = 370 – sukces. Teraz ułamek. Sposób konwersji ułamka binarnego na postać decymalną znajdziesz pod linkiem.

0.110010100011110 = 0.78997802734375

I co? Jest trochę mniej niż 0.79. I tu tkwi jedno z niebezpieczeństw związanych z float. Przy małej ilości operacji oraz małych wymogach co do precyzji np. jedno lub dwa miejscu po przecinku nie ma to aż tak dużego znaczenia, ale wyobraź sobie kiedy MCU wykonuje takich operacji setki lub tysiące i każda wprowadza taki mały błąd.

Z tego względu zapamiętaj: nigdy nie używaj operatorów == i != do porównywania liczb zmiennoprzecinkowych. Należy używać jakiejś małej delty, czy epsilon(różnie ludzie nazywają). Przykładowo: if( abs((oczekiwanie – wynik)) <= 0.01 )…

Dlaczego tak jest?

Precyzja

Wynik dodawania w powyższym przykładzie jest wynikiem precyzji liczb zapisywanych w zmiennej float. Myślisz, że możesz na nich zapisać wszystkie ułamki? Otóż nie. Przygotowałem w Octave wykres z zaznaczonymi floatami dla mantysy 8-bitowej oraz wykładnika od -5 do 5.

Każde kółko reprezentuje jedną liczbę. Co rzuca się w oczy? Co z wszystkimi liczbami między 0.5 a 1? Według tych parametrów jest ich tylko 4. Reszty nie ma. Oczywiście z mantysą i wykładnikiem zgodnymi ze standardem IEEE.754 pojawi się ich więcej ale to i tak nie pokryje wszystkich możliwych liczb.

Zauważ też, że im dalej od zera, tym rzadziej występują punkty. Domyślasz się co to oznacza? Operacje na wysokich liczbach przynoszą jeszcze większe błędy wynikające z tych ograniczeń.

Złożoność obliczeniowa i FPU

Dodawanie float wydaje się dosyć proste, ale zawiera kilka operacji jak wyciągnięcie wykładników, zrównanie ich, dodanie mantys i przekształcenia wyniku spowrotem do postaci IEEE.754. Podobnie jest z odejmowaniem, mnożeniem i resztą operacji. W porównaniu do obliczeń na liczbach binarnych wymagany jest spory narzut procesora. Innymi słowy wykonanie jednej operacji na liczbach zmiennoprzecinkowych wymaga wykonania przez MCU dziesiątek operacji, które wykonywane są za pomocą zwykłych działań binarnych.

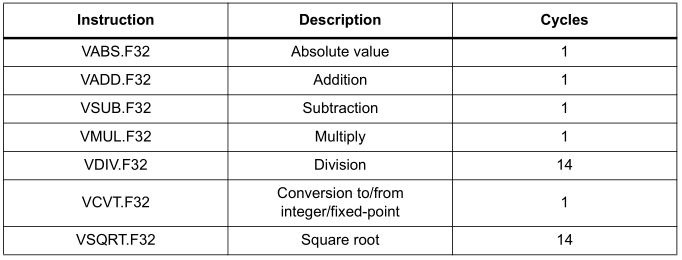
Niektóre mikrokontrolery wyposażone są w dodatkową jednostkę dedykowaną obliczeniom zmiennoprzecinkowym. Jest to FPU – Floating Point Unit. W tę jednostkę wyposażone są między innymi MCU z rodziny F4 oparte o rdzeń Cortex-M4 i Cortex-M7, czyli STM32 seria F4, L4, F7, H7. Jednostka ta robi dosłownie cuda z floatami. ST w swoich mikrokontrolerach oferuje z jej pomocą kilka sprzętowych działań na floatach pojedynczej precyzji:

Jak widzisz wartość bezwzględna, dodawanie, odejmowanie czy mnożenie realizowane jest tylko w jednym cyklu zegara. Te wszystkie operacje, które robiłem ręcznie, FPU robi za pstryknięciem cyfrowego palca. Dzielenie czy pierwiastkowanie to tylko 14 cykli. Dodatkowo widzimy w tabeli operacje konwersji typów zajmującą tylko jeden cykl. Magia? Trochę tak 🙂

To ile to to zajmuje Panie?

Naobiecywali tyle więc teraz sprawdźmy najważniejsze operacje za pomocą symulacji w IDE Keil µVision 5 na STM32F401RE, który mam w jednym ze swoich Nucleo. Biblioteka HAL której użyję jest w wersji 1.21. W ustawieniach projektu włączyłem symulator oraz ustawiłem brak optymalizacji. W kodzie zaraz po inicjalizacji HALa i zegarów wyłączam SysTick, aby nie zakłócał obliczeń. W pętli głównej napisałem prosty kod, który wykonuje podstawowe operacje na liczbach. Najpierw sprawdzę działanie na uint32_t, później float z wyłączonym FPU i z włączonym, a na końcu je porównam. Po każdym for’ze stawiam breakpoint i sprawdzam w symulacji stan licznika cykli zegara. Dla lepszej wizualizacji każdą operację wykonuję 100 razy. Niestety będzie trochę dodatkowych cykli przez pętle for, jednak dla każdej z opcji będzie to taka sama ilość, więc na wynik proporcjonalny nie wpłynie to mocno. FPU włącza/wyłącza się w ustawieniach projektu. W Eclipse(czy SW4STM32) będzie to w Project > Properties > C/C++ Build > Settings > MCU Settings pod rozwijanym menu o nazwie Floating point hardware.

uint32_t a = 6754;
uint32_t b = 1267;
uint32_t result;

//float a_f = 12.67;
//float b_f = 6.754;
//float result_f;

while (1)
{
	uint16_t i;
	// Add
	for(i=0; i<100; i++)
	{
		result = a+b;
		//result_f = a_f+b_f;
	}

	// Substract
	for(i=0; i<100; i++)
	{
		result = a-b;
		//result_f = a_f-b_f;
	}

	// Multiply
	for(i=0; i<100; i++)
	{
		result = a*b;
		//result_f = a_f*b_f;
	}

	// Divide
	for(i=0; i<100; i++)
	{
		result = a/b;
		//result_f = a_f/b_f;
	}

	// Modulo
	for(i=0; i<100; i++)
	{
		result = a%b;
		//result_f = fmod(a_f,b_f);
	}

	// Square root
	for(i=0; i<100; i++)
	{
		result = sqrt(a);
		//result_f = sqrtf(a_f);
	}

	//int to float
	for(i=0; i<100; i++)
	{
		result_f = (float)a;
	}

	//float to int
	for(i=0; i<100; i++)
	{
		result = (uint32_t)a_f;
	}

	result = result+1; // delete warning
	result_f = result_f+1; // delete warning
	/* USER CODE END WHILE */

	/* USER CODE BEGIN 3 */
}

Jesteś ciekaw wyników? Są interesujące.

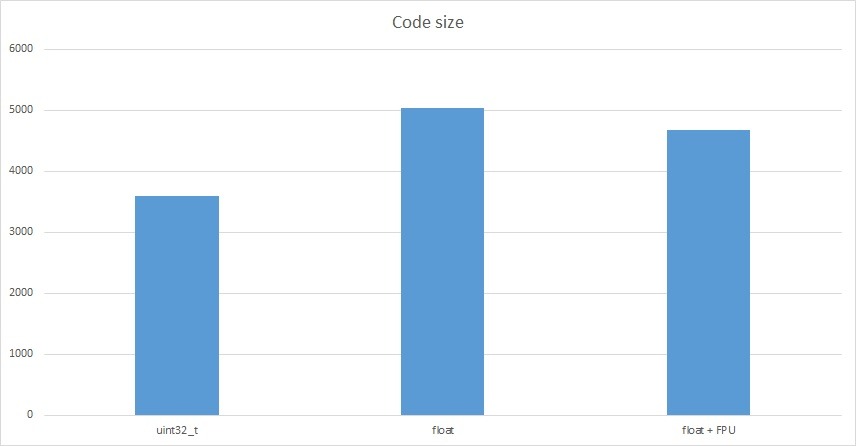
Na pierwszy ogień idzie rozmiar kodu wynikowego.

Typ zmiennych	Rozmiar w bajtach
uint32_t	3594
float bez FPU	5032
float z FPU	4684

Ilość dodatkowego kodu wynikająca z operacji na float wzrasta o niecałe 1,5 kB. Czy to dużo? Dla małych mikrokontrolerów AVR na pewno tak. STM32 mają dosyć sporą ilość pamięci Flash i uważam, że nie jest to wielkim problemem.

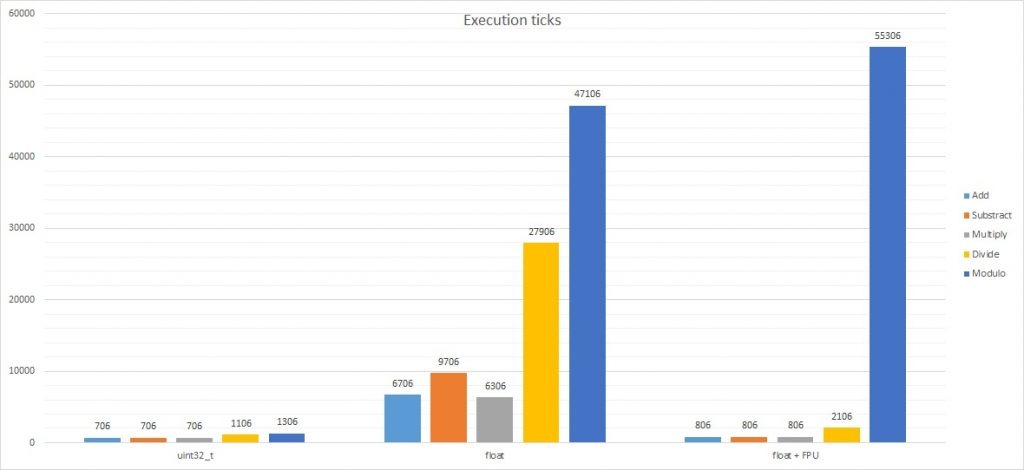
Teraz najciekawsze bo operacje na liczbach. Liczby w tabeli to ilość cykli zegara potrzebne do stukrotnego wykonania każdej z operacji.

Typ zmiennych	+	-	*	/	%	sqrt
uint32_t	706	706	706	1106	1306	211806
float bez FPU	6706	9706	6306	27906	47106	204306
float + FPU	806	806	806	2106	55306	4806

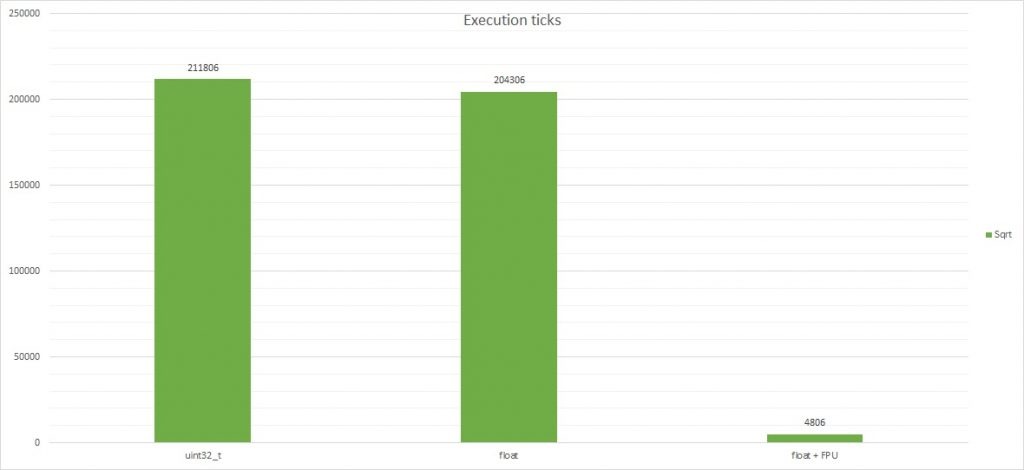
Ciekawe, nie? Wykres wspólny jest bardzo nieczytelny ze względu na ogromne wartości pierwiastkowania, dlatego rozbiję wyniki.

Czy widzisz już dlaczego wiele osób na forach denerwuje się gdy ktoś bez potrzeby używa floatów? Na razie porównajmy wyniki uint32_t vs float bez FPU. Nie każdy mikrokontroler ma FPU. Tym bardziej popularne Arduino, gdzie gotowe biblioteki pchają float gdzie popadnie. Czas obliczeń float jest wolniejszy od uint32_t:

• ~9.5 razy przy dodawaniu
• ~13.75 razy przy odejmowaniu
• ~8.93 razy przy mnożeniu
• ~25.23 razy przy dzieneniu!
• ~36 razy przy modulo!

Co ciekawe liczenie pierwiastka kwadratowego zajmuje podobną ilość cykli zegara. Poszperałem trochę w dokumentacji rdzenia M4. Nie posiada on instrukcji do pierwiastkowania binarnego stąd pewnie taki narzut. Biblioteka musi poradzić sobie za pomocą podstawowych działań zarówno dla uint32_t jak i float. Teraz zerknij na pierwiastkowanie za pomocą FPU. Robi wrażenie, co nie? Jednostka zmiennoprzecinkowa posiada już instrukcje specjalnie do tej operacji. Potrafi ją wykonać błyskawicznie(~42 razy szybciej) w porównaniu do uint32_t i float bez FPU.

Co dało włączenie FPU?

Ilość potrzebnych cykli CPU dla obliczeń float niemal zrównała się z tymi dla uint32_t. Wyjątkiem jest operacja modulo. Wynika to z prostego powodu. FPU nie wspiera dzielenia modulo, stąd w bibliotekach wymagany jest narzut obliczeniowy za pomocą innych operacji takich jak dodawania, odejmowanie, mnożenie, dzielenie. Tutaj nic nie ugramy a nawet jak pokazuje wykres – przegramy. Nie potrafię wytłumaczyć dlaczego modulo float przy włączonym FPU potrzebowało jeszcze więcej cykli zegara niż obsługa jedynie softowa. Nie zagłębiałem się w biblioteki CMSIS i instrukcje CPU. Może któryś z czytelników ma większą wiedzę w tym zakresie i podzieli się w komentarzu?

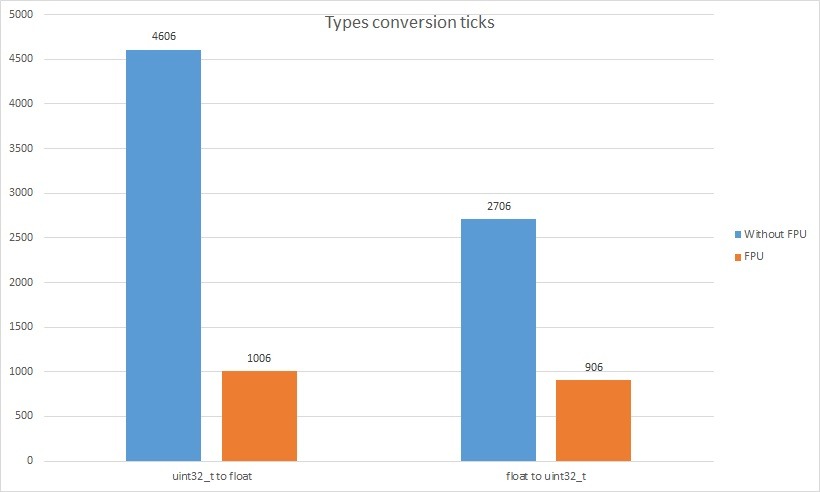
Pozostała jeszcze konwersja typów.

Typ operacji	Bez FPU	FPU
uint32_t to float	4606	1006
float to uint32_t	2706	906

Zysk z zastosowania FPU do konwersji typów jest bezapelacyjny i myślę, że nie wymaga komentarza. Dla pierwiastkowania opłaca się przekonwertować inty na float, policzyć i przekonwertować spowrotem. Należałoby sprawdzić czy dokładność reprezentacji float będzie wystarczająca dla zastosowania.

Jak żyć?

Pisząc progamy lepiej zastanowić się czy liczby zmiennoprzecinkowe są nam niezbędne. Często pada stwierdzenie, że “przecież tutaj nie ma to znaczenia” gdy dyskusji poddawany jest jakiś mały program początkującego programisty. Dyskusja rośnie czasami do rozmiarów tych pod tytułem “PC vs konsola”. Ja mam takie zdanie, że wszędzie tam, gdzie się da powinno unikać się float. Nigdy nie wiesz kiedy pisząc kobylastą bibliotekę na floatach będziesz chciał wywoływać te operacje setki razy na sekundę. Wtedy MCU może się przytkać. Oczywiście są zastosowanie, gdzie liczby zmiennoprzecinkowe są niezbędne i należy być świadomym częstego używania float.

Często można sobie poradzić inaczej niż floatem. Przykład: a /= 2.55 będzie równoznaczne z a = (a * 100)/255 wykonanym na uintach. Czasem trzeba wykonać to na intach nie 8-bitowych a 16, 32 lub nawet 64. Będzie to nadal dużo szybsze a MCU Ci za to odwdzięczy się w prędkości działania. Chyba, że w gre wchodzą tak duże liczby, że zakres 64 bitów jest za mały.

Unikałbym dzielenia modulo na floatach. Na szczęście rzadko jest to używane. Ja sam nigdzie nie używałem tego typu operacji. Ktoś może podać praktyczne zastosowanie?

Zyskać można natomiast na pierwiastkowaniu floatami po zapięciu FPU. Konwersja typów trwa wtedy jeden cykl, a pierwiastkowanie kilkanaście. To będzie zdecydowanie szybsze niż biblioteczne liczenie pierwiastka na uintach.

A Ty jaką masz opinię?

Podsumowanie

Mam nadzieję, że choć trochę rozumiesz dlaczego używanie floatów na mikrokontrolerach budzi tyle emocji. Temat jest ciekawy i mam nadzieję, że zaszczepiłem w Tobie chęć doczytania np. o dzieleniu float, overflow lub underflow czy może innych pułapkach liczb zmiennoprzecinkowych. Jeżeli chciałbyś dowiedzieć się więcej, polecam na przykład prezentacje Pułapki liczb zmiennoprzecinkowych gdzie autor opisał więcej zagadnień związanych z floatami. W Internecie znajduje się wiele fajnych publikacji na ten temat.

Dziękuję Ci za przeczytanie tego wpisu. Jeśli taka tematyka Ci odpowiada, daj mi znać w komentarzu. Będę też wdzięczny za propozycję tematów które chciałbyś abym poruszył.

Jeśli zauważyłeś jakiś błąd, nie zgadzasz się z czymś, chciałbyś coś dodać istotnego lub po prostu uważasz, że chciałbyś podystkutować w tym temacie, napisz komentarz. Pamiętaj, że dyskusja ma być kulturalna i zgodna z zasadami języka polskiego.